Wybrane prace naukowo-badawcze
Prace nad wpływem przewozu niskotemperaturowego ładunku na rozkład temperatury w elementach konstrukcyjnych kadłuba statku. Obecnie gaz LNG (z ang. liquified natural gas) jest coraz częściej przewożony drogą morską przy pomocy specjalnie do tego przystosowanych statków. Dodatkowo LNG zyskuje coraz większą popularność jako paliwo napędowe w porównaniu do klasycznych paliw ciężkich, głównie dzięki dużo mniejszej emisyjności dwutlenku węgla. Coraz częściej na innych typach statków (np. promach pasażersko-samochodowych) montuje się zbiorniki do przewozu skroplonego gazu.
Gaz LNG przyjmuje formę ciekłą w niskiej temperaturze: około –163°C. Może to generować szereg kłopotów związanych z integralnością konstrukcji kadłuba. Mimo że stosuje się izolację pomiędzy ładunkiem oraz elementami konstrukcyjnymi kadłuba, to i tak kadłub narażony jest na działanie niskich temperatur. W takich sytuacjach tradycyjna stal kadłubowa może stawać się krucha, a to zwiększa jej podatność na pękanie. Dodatkowo niskie temperatury powodują kurczenie się stalowych elementów, co może prowadzić do wysokich naprężeń w konstrukcji. Rozwiązaniem problemu negatywnego oddziaływania niskich temperatur może być zastosowanie w tych rejonach kadłuba innych gatunków stali, tj. takich o niskiej temperaturze przejścia w stan kruchy oraz niskim współczynniku rozszerzalności cieplnej.
W procesie projektowania konstrukcji statku do przewozu zbiorników LNG należy wstępnie określić rozkład temperatury w kadłubie, aby odpowiednio dobrać rodzaj stali. Jedną z metod jest wykonanie obliczeń analitycznych. W przypadku wielu elementów konstrukcyjnych, tworzących otoczenie zbiorników LNG, obliczenia analityczne mogą być dość skomplikowane. Alternatywną metodą będą symulacje numeryczne z wykorzystaniem Metody Elementów Skończonych. W ramach prac badawczo-rozwojowych prowadzonych w PRS, wykorzystywano obie metody tego typu obliczeń. Wyniki obu metod zostały ze sobą porównane.
Przykład rozkładu temperatury w rejonie dna podwójnego typowego statku do przewozu LNG pokazany został na poniższym rysunku:

Rys. 1. Rozkład temperatury w konstrukcji dna podwójnego statku LNG [°C].
Rozwiązano zagadnienie rozkładu temperatury w elementach konstrukcji przy założeniu, że temperatura w zbiorniku ładunkowym, sąsiadującym ze zbiornikami balastowymi, wynosiła –163°C. Pomiędzy konstrukcją kadłuba a zbiornikiem zamodelowano jeszcze warstwę izolacji. W obliczeniach uwzględnione zostały dwa mechanizmy transferu ciepła (konwekcja i kondukcja) [1, 2]. Kondukcja powoduje transfer ciepła wewnątrz elementów stalowych, natomiast konwekcja odpowiada za transfer ciepła wewnątrz zbiorników balastowych. Zbiorniki te mogą być puste lub wypełnione wodą balastową, więc w obu przypadkach należy przyjąć inne własności termiczne. Również własności termiczne stali należy odpowiednio określić [3]. Na styku kadłuba zewnętrznego z wodą zaburtową przyjęto temperaturę 0°C (wg wymagań Kodeksu IGC [4]). Na podstawie obliczeń uzyskano rozkład temperatury na kadłubie statku, jak pokazano na rys. 1.
W porównaniu z metodą analityczną, modelowanie MES pozwala uzyskać wyniki dużo szybciej. Dodatkowo możliwe jest przeprowadzenie obliczeń 3D (tj. z uwzględnieniem grodzi poprzecznych).
Na podstawie przeprowadzonych prac badawczo-rozwojowych zostaną opracowane wytyczne do prowadzenia tego typu obliczeń.
Literatura
[1] von Böckh P., Wetzel T. Heat Transfer. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012.
[2] Annaratone D. Engineering Heat Transfer. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010.
[3] Marquardt ED, Le JP, Radebaugh R. Cryogenic Material Properties Database. Cryocoolers 11, Boston, MA: Springer US, 2002, p. 681–7.
[4] International Maritime Organization. International Code for the Construction and Equipment of Ships Carrying Liquefied Gases in Bulk. London: IMO, 2016.
W artykule [1] przedyskutowano wpływ podziału przestrzennego statku na stateczność w stanie awaryjnym. Promy starego typu miały podział przestrzenny podobnie, jak narysunku 1, charakteryzujący się tym, że przestrzeń poniżej pokładu samochodowego była gęsto podzielona grodziami poprzecznymi. Większość przedziałów była pusta, nie używana do przewozu jakiegokolwiek ładunku. Nie było podwójnych burt powyżej pokładu samochodowego. Taki typ podziału grodziowego był powszechnie stosowany do końca lat dziewięćdziesiątych.
Obecnie, przestrzeń poniżej pokładu samochodowego jest często przeznaczona do przewozu ładunku typu ro-ro w postaci długiej ładowni (Long Lower Hold – LLH), rozciągającej się na około połowie długości promu. Poniżej pokładu samochodowego są podwójne burty podzielone grodziami poprzecznymi, zwykle sięgającymi pokładu samochodowego. Nie ma grodzi poprzecznych w przestrzeni ładunkowej. Dla poprawienia bezpieczeństwa podwójne burty powinny rozciągać się powyżej pokładu samochodowego – patrz [2, 3].
Analiza zawarta w raporcie została wykonana używając za punkt wyjściowy zmodyfikowany na potrzeby obliczeń prom zbudowany w roku 1990, jeszcze używany.
Statek spełnia wymagania rezolucji IMO A.265 [4], poprzednika obecnej zharmonizowanej Konwencji SOLAS [5]. Powyższa Rezolucja nie wymaga rezerwowej wyporności powyżej pokładu samochodowego. W przypadku istnienia LLH pod pokładem samochodowym, szerokość podwójnych burt pod pokładem samochodowym powinna być równa b = 0.2B, natomiast wysokość dna podwójnego powinna wynosić co najmniej hb = 0,1B. Trzeba zaznaczyć, że podwyższona wysokość dna podwójnego jest szkodliwa dla stateczności statku w stanie awaryjnym [1]. Ze względu na bezpieczeństwo po uszkodzeniu dno podwójne powinno być położone najniżej, jak to możliwe. Minimalna wysokość dna statku badanego, zgodnie z Przepisami PRS wynosi
HB = 1.025 m.
Bibliografia
- Pawłowski M., Laskowski A. Effect of watertight subdivision on damage stability of ro-ro ferries, Trans RINA, Vol. 156, Part A2, Intl J Maritime Eng, Apr–Jun 2014, pp. A-131–136, DOI No: 10.3940/rina.ijme.a2.2014.283.
- Pawłowski M. Subdivision of RO/RO ships for enhanced safety in the damaged condition, Marine Technology, Vol. 36, No. 4, Fall 1999, pp. 194–202.
- RINA, Best Ships of 2001, pp. 46-47.
- International Maritime Organisation: Regulations on subdivision and stability of passenger ships (as an equivalent to part B of chapter II of the 1960 SOLAS Convention), London, IMO, 1974. This publication contains IMO resolution A.265 (VIII), A.266 (VIII) and explanatory notes.
- International Maritime Organisation: SOLAS Convention, Consolidated Edition 2009, IMO, London 2009.
- ROROPROB (2000–2003) Probabilistic rules-based optimal design of ro-ro passenger ships, EU Research Project, FP5, DG XII-BRITE.
- Ravn Erik Sonne, Probabilistic Damage Stability of Ro-Ro Ships, Phd Thesis, Technical University of Denmark, Department of Mechanical Engineering, Maritime Engineering, Denmark, Kongens Lyngby 2003.
W Pionie Naukowo-Badawczym została wykonana praca badawcza dotycząca sił w łańcuchach cumowniczych.
Łańcuch górnym końcem B przymocowany jest do jednostki cumowanej, a dolnym zakotwiczony jest na dnie, jak na Rys. 1. Zakładamy, że dno na głębokości h jest poziome. Łańcuch spoczywa na dnie na pewnym odcinku xA. Początek układu znajduje się na końcu części spoczywającej w punkcie A,. Kotwica może przenosić jedynie siły poziome. Dlatego istotne jest, by xA > 0, tj. by długość spoczywającej części łańcucha nigdy nie spadła do zera podczas kotwiczenia. Łańcuch jest cięgnem ciężkim.
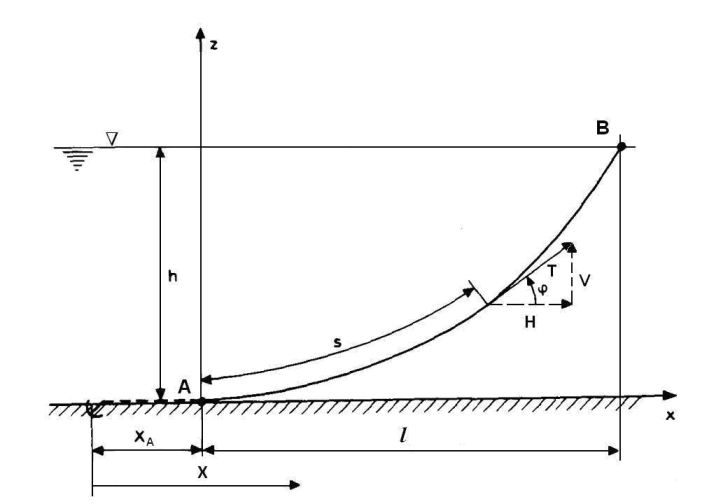
Rys. 1. Symbole użyte do analizy cięgna
Podstawowe zależności
Równaniem linii łańcuchowej przechodzącej przez początek układu jest krzywa łańcuchowa, dana wzorem:
z = m(coshx/m – 1),
gdzie m º H/q, H jest składową poziomą naciągu łańcucha, stałą wzdłuż zwisającego łańcucha, zaś q jest jednostkowym ciężarem łańcucha, z uwzględnieniem wyporu. Zadając współrzędne punktu B(l, h), otrzymamy równanie na nieznany parametr m:
h = m(coshl/m – 1).
Pozioma długość części zwisającej łańcucha l jest zwykle 5¸20 razy większa od głębokości h.
W analizie łańcucha, wygodnie jest stosować wielkości bezwymiarowe, odniesione do stałej głębokości akwenu h, która jest znana. Wprowadzając oznaczenia: u º m/h, v º l/h, otrzymamy równanie na bezwymiarowy naciąg łańcucha u = m/h º H/qh:
1/u = coshv/u -1 (1)
Z równania wynika, że bezwymiarowy naciąg u jest funkcją zmiennej v = l/h, pokazaną na Rys. 2 linią ciągłą. Kółkami zaznaczona jest aproksymacja kwadratowa tej funkcji: u = ½v2. Widać, że w kategoriach absolutnych jest dobra w całym zakresie l/h.
Wzór (1) pozwala łatwo wyznaczyć składową poziomą napięcia cięgna H, gdy znamy głębokość h, stosunek l/h = v i masę jednostkową łańcucha r. Przykładowo, gdy v º l/h = 10, otrzymamy, że m/h º H/qh = ½102 = 50. Stąd, składowa pozioma napięcia H = 50qh. Na akwenie o głębokości h = 150 m i masie jednostkowej łańcucha r = 150 kg/m, pozioma składowa napięcia wynosi H = 11036 kN. Gdyby l/h = 5, składowa H byłaby 4 razy mniejsza.
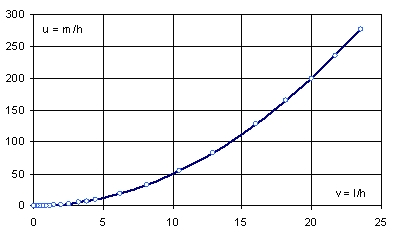
Rys. 2. Zależność parametru u º m/h = H/qh od zmiennej v = l/h
Znając parametry m i l, długość zwisającej części łańcucha dana jest wzorem: s = msinhl/m, lub w formie bezwymiarowej: s/h = usinhv/u. Funkcja ta przedstawiona jest na Rys. 3.
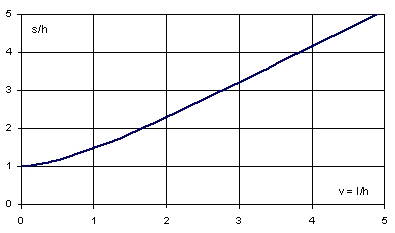
Rys. 3. Zależność bezwymiarowej długości liny s/h od zmiennej v = l/h
Nachylenie łańcucha w dowolnym punkcie dane jest wzorem: tgj = s/m = sinhx/m. Maksymalne nachylenie na końcu łańcucha w punkcie B wynosi: tgj = sinhl/m.
Napięcie łańcucha T w dowolnym punkcie określa wzór: T = q(m + z). W punkcie B na końcu łańcucha, napięcie wynosi: T = q(m + h), lub w formie bezwymiarowej: T/qh = 1 + u.
Z Rys. 2 widać, że zmiana poziomej długości zwisającego łańcucha, np. wywołana ruchami statku, skutkuje zmianą składowej poziomej napięcia i kształtu zwisającego łańcucha (Rys. 4).
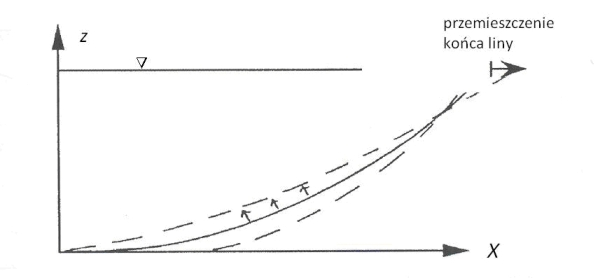 Rys. 4. Zmiana kształtu cięgna wywołana przemieszczaniem końca
Rys. 4. Zmiana kształtu cięgna wywołana przemieszczaniem końca
Sztywność napięcia łańcucha
Pochodna dH/dl = qv = 2H/l, gdzie v º l/h, jest współczynnikiem sztywności łańcucha. Im większy jest ciężar jednostkowy łańcucha q i stosunek l/h, tym sztywniejsze jest napięcie łańcucha.
W zastosowaniach potrzebna jest sztywność napięcia łańcucha względem przemieszczenia statku dX, czyli względem przemieszczenia punktu B na końcu łańcucha. Dana jest ona wzorem:
dH/dX = 1,5v3q.
Wzór powyższy, ściśle rzecz biorąc, ważny jest dla małych przemieszczeń łańcucha w punkcie B. Dla skończonych przemieszczeń DX zmiana poziomego napięcia łańcucha DH wyraża się wzorem:
DH = 1,5v03(1 + e)(1 + ½e)qDX,
gdzie v0 º l0/h jest początkową wartością stosunku l/h, e = Dl/l0 º Dv/v0 jest względną zmianą długości liny, równą: e = 1,5vDX/h. Dzieląc powyższy wzór przez qh, otrzymamy postać bezwymiarową:
Du = 1,5v03(1 + e)(1 + ½e)DX/h.
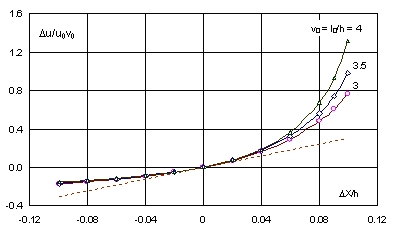
Wykres tej wielkości w funkcji względnego przemieszczenia końca liny DX/h przedstawiony jest na Rys. 5 dla trzech wartości stosunku v = l/h = 3, 3,5, 4.
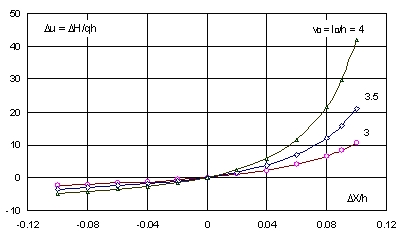
Rys. 5. Wpływ przemieszczenia końca łańcucha na zmianę siły przywracającej
Widać, że siła przywracająca H zmienia się nieliniowo zwłaszcza, gdy koniec liny oddala się od zakotwiczenia, przy czym nieliniowość wzrasta ze wzrostem stosunku v º l/h. Pochodna w zerze (Du)’ = 1,5v03. Iloczyn
(1 + e)(1 + ½e) = Du/Dul
przedstawia wpływ nieliniowości na sztywność łańcucha. Wykres Du/Dul = (1 + e)(1 + ½e) w funkcji względnego przemieszczenia końca liny DX/h przedstawiony jest na Rys. 6 dla trzech wartości stosunku v = l/h = 3, 3,5, 4. Gdyby zmiana siły przywracającej była liniowa, tj. proporcjonalna do przemieszczenia, stosunek Du/Dul byłby równy 1. Z wykresu widać, że gdy przemieszczenie DX = 8%h, to przyrost siły przywracającej dla v = l/h = 3 jest dwukrotnie większy, niż to by wynikało z teorii liniowej, a dla l/h = 4 prawie trzykrotnie. Pochodna w zerze (Du/Dul)’ = 2,25v. Styczna o tym współczynniku pokazana jest na Rys. 6 linią przerywaną dla v0 = 3.
Względny przyrost siły przywracającej Du/u º DH/H dany jest wzorem: Du/u0 = 3v0(1 + e)(1 + ½e)DX/h. Widzimy, że jest on proporcjonalny do v0 = l0/h. Zatem, dzieląc Du/u0 przez v0, otrzymamy:
Du/u0v0 = 3(1 + e)(1 + ½e)DX/h.
Wykres tej wielkości w funkcji względnego przemieszczenia końca liny DX/h przedstawiony jest na Rys. 7. Są to krzywe dość silnie wygięte zwłaszcza, gdy DX > 0 Pochodna w zerze (Du/u0v0)’ = 3, jest stała, niezależna od v. Oznacza to, ze w sąsiedztwie zera wszystkie krzywe mają wspólny przebieg.
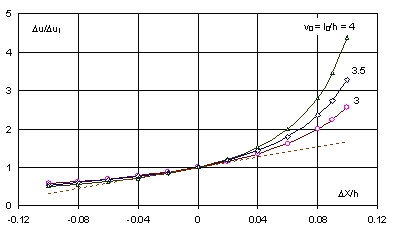
Rys. 6. Nieliniowość sztywności łańcucha
 Rys. 7
Rys. 7
Gdyby sztywność liny była stała, wówczas Du/uv = 3DX/h; wykresem tej wielkości byłaby linia prosta o współczynniku kierunkowym 3, pokazana linią przerywaną na Rys. 7. Jest ona styczna do krzywych w początku układu. Widać, że nieliniowość sztywności liny można zaniedbać, gdy przemieszczenia końca liny DX w płaszczyźnie poziomej nie przekraczają ±0,04h, czyli gdy nie przekraczają 4% głębokości akwenu h.
Analogiczne zależności można otrzymać z rozważań energetycznych.
Działające siły
Na zacumowany obiekt mogą działać siły od:
- wiatru
- i lodu.
- prądu
- falowania
Cumy dobiera się na ekstremalne warunki, jakie mogą wystąpić w okresie 100 lat. Dla Morza Północnego stuletnia średnia prędkość wiatru na wysokości h = 10 m n.p.m. wynosi u = 41 m/s, czyli 148 km/h.
Przyjmuje się, że w okresie 20-25 lat eksploatacji statek napotyka na 108 fal. Zatem, w okresie 100 lat daje to około 4,5×108 = 108,7 oscylacji.
Dla typowego okresu eksploatacji statku 20-25 lat szukamy poziomu odpowiedzi statku przekraczanego z prawdopodobieństwem Pa = 10–8, czyli średnio raz w okresie eksploatacji statku, a w wypadku obiektów oceanotechnicznych – poziomu przekraczanego z prawdopodobieństwem Pa = 10–8,7, czyli średnio raz na 100 lat. W tym ostatnim przypadku możemy mówić o amplitudzie stuletniej.
Napór falowania
Napór wywołany falowaniem najprościej jest oszacować metodą Gerritsmy–Beukelmana na obliczanie przyrostu oporu na fali regularnej. Jest ona ważna także dla statku zacumowanego, dany wzorem:
RAW = (wkòLb33Yw2dx)½z02.
Wyrażenie w nawiasie ma wymiar kg/ms2, identyczny jak iloczyn ciężaru właściwego i długości. Wyciągając przed nawias gB2/L, gdzie g = rg jest ciężarem właściwym wody, zaś B i L to wymiary główne statku, otrzymamy bezwymiarowy współczynnik dodatkowego oporu na fali regularnej rAW, zależny od częstości fali w, a niezależny od amplitudy fali:
rAW = (kwòLb33Yw2dx)/g(B2/L).
Z pomocą tego współczynnika, przyrost oporu wyrazi się wzorem:
RAW = rAWg(B2/L)½z02,
Przejście na falę nieregularną jest proste. Uwzględniając, że ½z02 = S(w)dw, stąd,
RAW = g(B2/L)òrAWS(w)dw.
Napór falowania można więc obliczyć teoretycznie, w oparciu o znajomość współczynnika tłumienia dla nurzań b33 dla przekrojów wręgowych i funkcji przenoszenia ruchów względnych wręgu Yw. Bezwymiarowy współczynnik przyrostu oporu na fali regularnej rAW można znaleźć też za pomocą badań modelowych oporu okrętu na fali regularnej, w oparciu o wzór: rAW º RAW/g(B2/L)½z02.
Do celów szacunkowych dogodny jest przedostatni wzór, gdzie rAW jest średnim bezwymiarowym współczynnikiem dodatkowego oporu na fali nieregularnej, a ½z02 zastąpione jest wariancją m0 = (¼Hs)2 dla najwyższego stanu morza. Dla Morza Północnego Hs = 13,5 m. Można przyjąć wstępnie, że rAW » 2.
Siła wywołana prądem
Siłę tę obliczamy tak, jak dla statku na wodzie spokojnej poruszającego się z prędkością, jak prąd. Ze względu na stosunkowo niewielkie prędkości prądu siła ta redukuje się do oporu lepkości, danego wzorem:
Rcx = cFr½u2W,
gdzie r jest gęstością wody w kg/m3, u jest prędkością prądu w m/s, W jest powierzchnią zwilżoną kadłuba w m2, zaś cF jest współczynnikiem tarcia płaskiej płyty:
cF = 0,075/(lgRe – 2)2,
gdzie Re = uL/n jest liczbą Reynoldsa, L jest długością statku w m, zaś n jest kinematycznym współczynnikiem lepkości wody w m2/s. W wypadku ukośnego ustawienia statku względem kierunku prądu, bierzemy składową podłużną prędkości.
Przy poprzecznym ustawieniu statku względem prądu, siła oporu dana jest wzorem:
Rcy = cD½ru2LT,
gdzie T jest średnim zanurzeniem statku, zaś cD » 0,6 jest współczynnikiem oporu.
Siła wywołana wiatrem
Siła ta równa się oporowi powietrza, jaki działa na nadwodną część statku. Wzór na opór powietrza przyjmuje następującą postać:
RA = cA½rAuA2AT,
gdzie r jest gęstością wody w kg/m3, uA jest prędkością wiatru w m/s, AT jest powierzchnią rzutu wręgowego nadwodnej części kadłuba w m2, zaś cA » 0,6 jest współczynnikiem oporu powietrza.
Maksymalne wykorzystanie możliwości ładunkowych przy minimalnych naprężeniach i spełnionych wymogach stateczności jednostki to ideał z punktu widzenia zarówno bezpieczeństwa, jak i opłacalności w eksploatacji. Jednym z celów prac naukowo-badawczych prowadzonych w PRS jest tworzenie numerycznych modeli oraz programów komputerowych, służących do przeprowadzania potrzebnych analiz i symulacji zachowania się statku, jego konstrukcji i wyposażenia w normalnych oraz ekstremalnych warunkach eksploatacyjnych. Program StabPRS służący do kontroli stateczności, wytrzymałości ogólnej w dowolnym stanie załadownia, jest jednym z takich programów.
PRS oferuje swoim klientom aplikację szytą na miarę dla każdego typu statku, w tym również zbiornikowca, która pozwala między innymi określić parametry optymalnego ładunku, rozmieszczenie balastu, ułatwiając pracę osób odpowiadających za załadunek/ wyładunek i bezpieczny transport.
Program nie wymaga szczególnego środowiska. Możliwość szybkiego przetwarzania danych, zaciąganie informacji z sensorów, instrumentów pomiarowych na statku, sprzyjają korzystaniu z kalkulatora zarówno w codziennych, jak i w awaryjnych warunkach. Graficzna postać stanu zbiorników, wbudowane instrukcje pomocnicze dla użytkowników oraz archiwizacja danych i wyników obliczeń na życzenie czynią program przyjaznym i przejrzystym dla użytkownika. Miejsce archiwizacji danych i obliczeń oraz wydruki, jak również przesyłanie danych pozostają pod pełną kontrolą użytkownika.
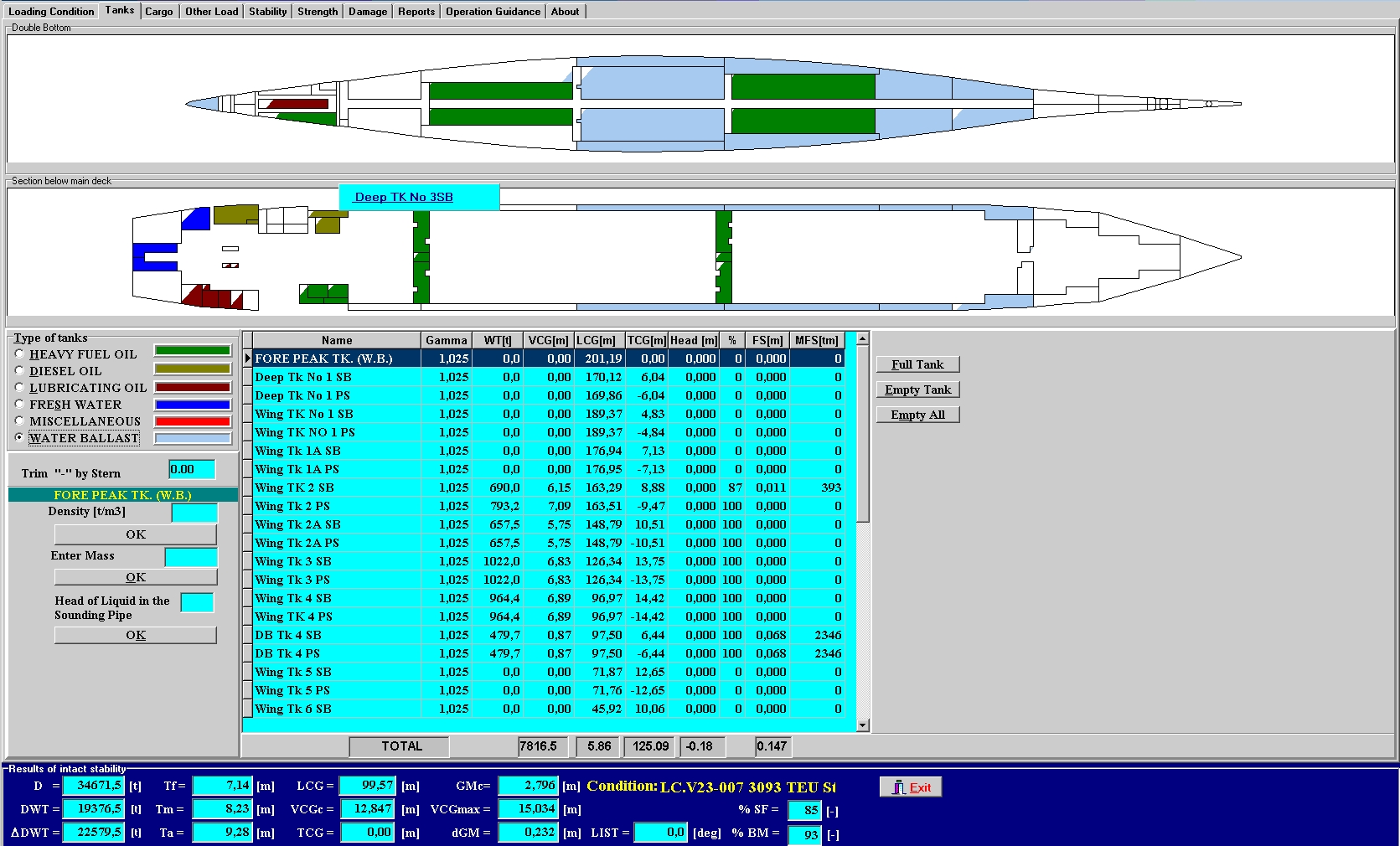
Program pozwala na określenie masy ładunku przyjętego lub wyładowanego ze statku na podstawie zanurzenia jednostki (tzw. Draft Survey). Obliczenia statecznościowe statku w stanie nieuszkodzonym i uszkodzonym uwzględniają kryteria IMO.
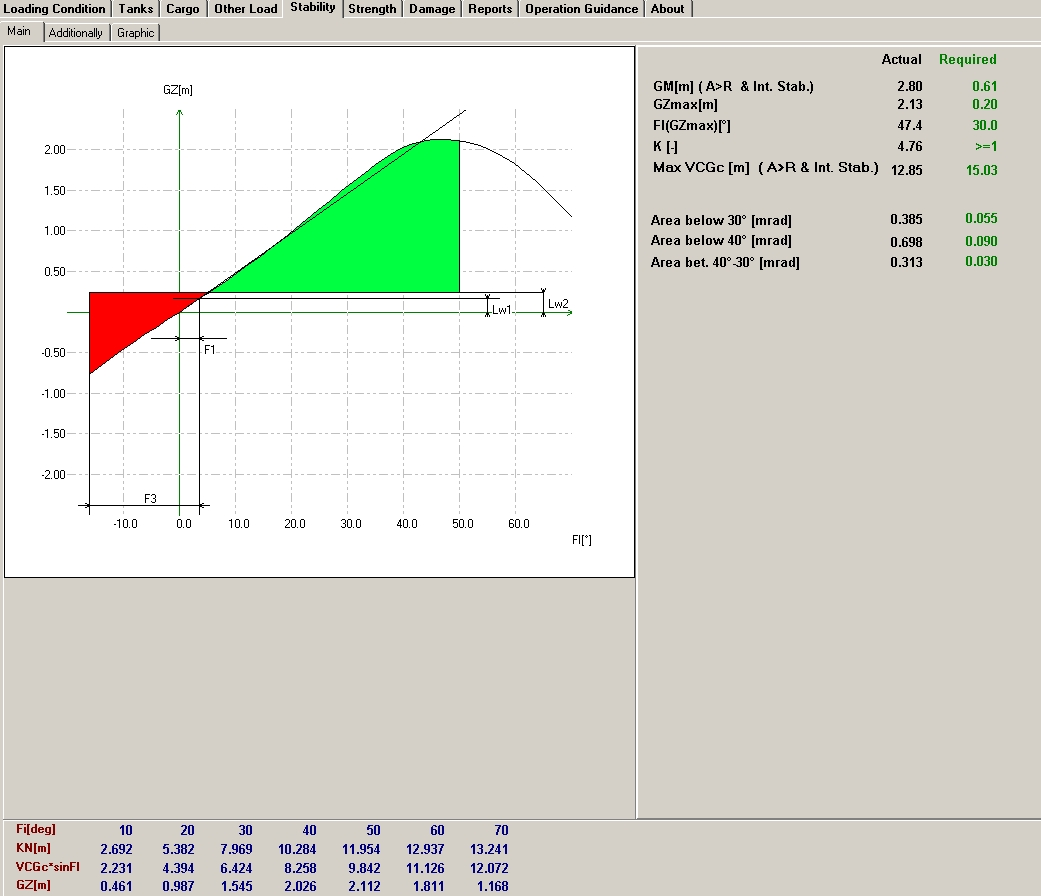
Dynamiczny, graficzny interface przystosowany do danej jednostki oraz wizualizacja wyników i obciążeń na dany moment ułatwią pracę.
Modele obliczeniowe
W Pionie Naukowo-Badawczym przeprowadzono badania nad wytrzymałością kadłuba kontenerowca poddanego obciążeniom skręcającym. Przeanalizowano dwie metody przeprowadzania obliczeń: opracowaną w Polskim
Rejestrze Statków metodę opartą o model globalny kadłuba oraz metodę analogiczną do wymaganych przez przepisy Common Structural Rules dla masowców i zbiornikowców, opartą o model ograniczony do modułu trzech ładowni (tzw. ‘cargo-hold analysis’).
Poniżej przedstawiono siatkę elementów skończonych analizowanego statku, na podstawie której utworzono modele zgodne z wymaganiami obu metod.
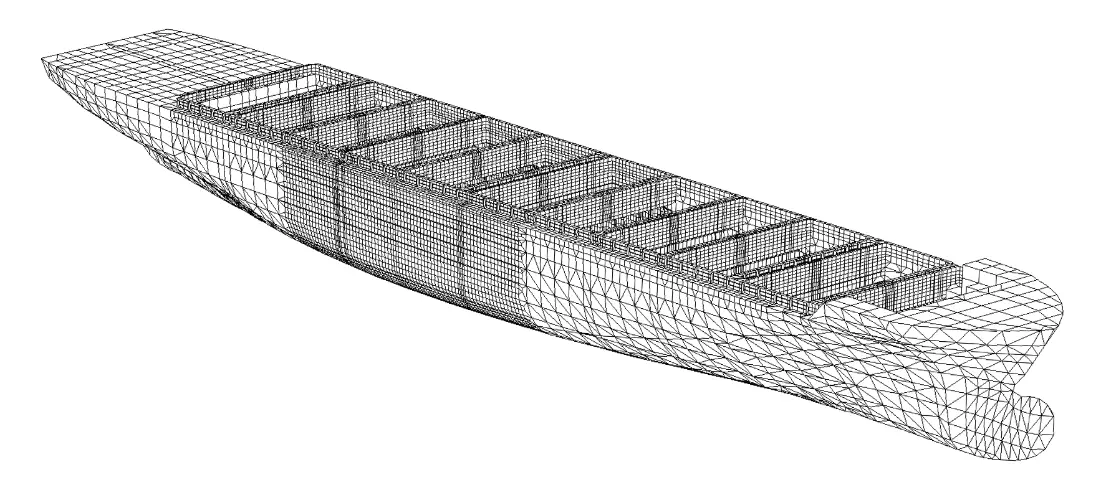
Rys. 1. Siatka elementów skończonych kontenerowca
Pierwszy z utworzonych modeli, zgodny z opracowaną w Pionie Naukowo-Badawczym metodą, to model globalny z siatką elementów skończonych podzieloną na dwa rejony. W rejonie trzech ładowni na śródokręciu siatka zbudowana jest z elementów płytowych o wymiarach rzędu odstępu między kolejnymi usztywnieniami, natomiast w częściach skrajnych kadłuba elementy są rozpięte pomiędzy kolejnymi wiązarami. Dodatkowo, w rejonie środkowym zamodelowano usztywnienia poszycia w postaci elementów belkowych. Obciążenie skręcające zrealizowano przy pomocy stałych przedziałowo obciążeń ciągłych, przyłożonych do burt modelu. Model przedstawiono na poniższym rysunku.
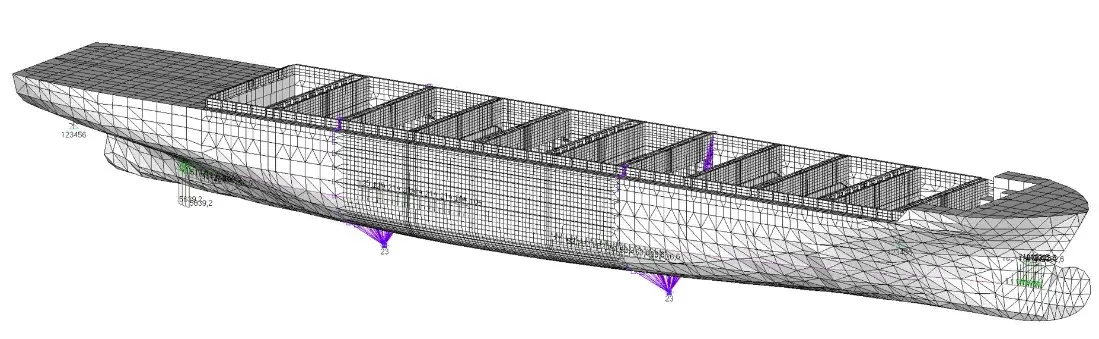
Rys. 2. Model A, oparty o opracowaną w PRS metodę
Drugi model, który powstał w oparciu o przepisy CSR, ograniczony jest po długości do modułu trzech ładowni na śródokręciu (fragment z zagęszczoną siatką widoczny na Rysunku 3). Siatka elementów skończonych składa się z elementów płytowych wielkości odstępu między kolejnymi usztywnieniami oraz elementów belkowych reprezentujących usztywnienia. Sztywność skrajnych części kadłuba zasymulowano za pomocą tzw. ‘end-constraint beams’. Model obciążono przy pomocy skupionego momentu skręcającego.
Wyniki obliczeń
Postać deformacji obu modeli, przedstawiona na rysunkach 3 oraz 4, zgadza się ze wstępnymi prognozami oraz oddaje charakter zadanego obciążenia skręcającego. W obu przypadkach wyraźnie widoczna jest deplanacją przekrojów modelu, w modelu B jest on jednak znacznie bardziej wydatny.
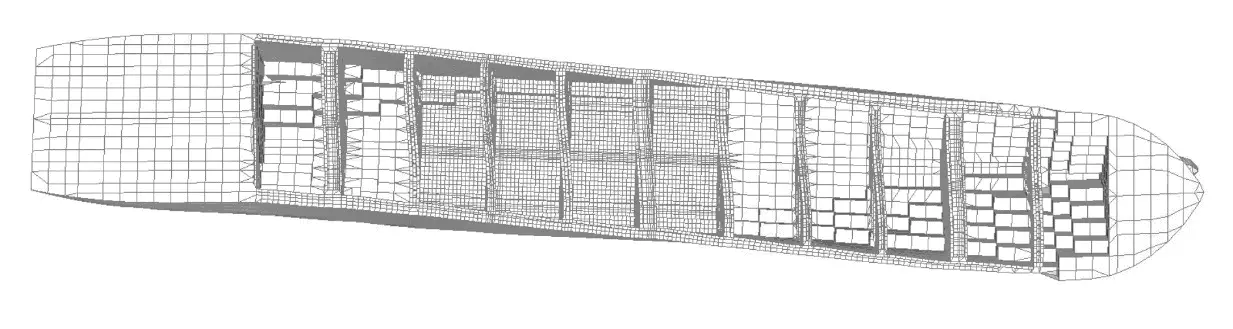
Rys. 3. Postać deformacji modelu A
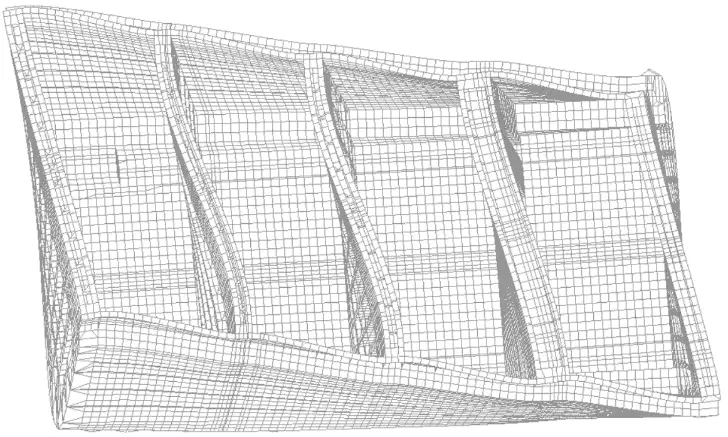
Rys. 4. Postać deformacji modelu B
Rozkład naprężeń w obu modelach jest podobny, z koncentracją występującą w charakterystycznych miejscach, a więc w narożach luków oraz w poszyciu pokładów w rejonie przewiązki międzylukowej. Znaczne różnice występują natomiast w wartościach naprężeń, które w modelu B są znacznie zaniżone.
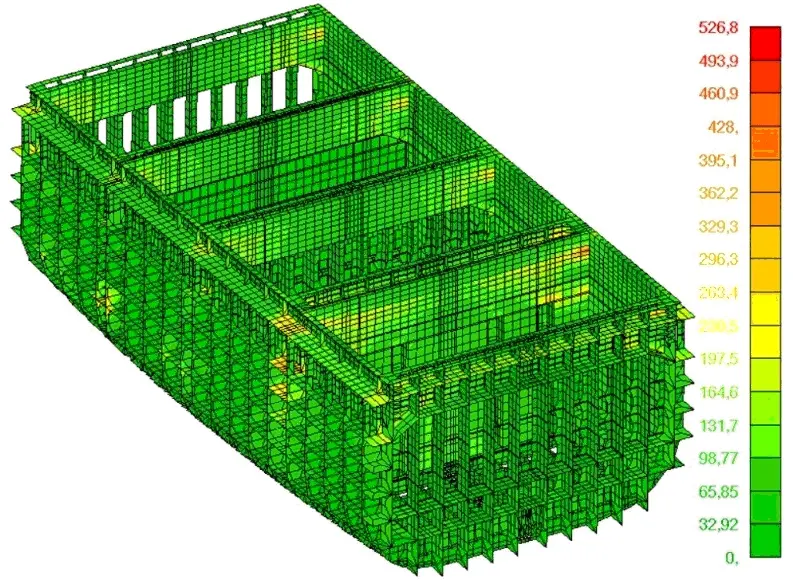
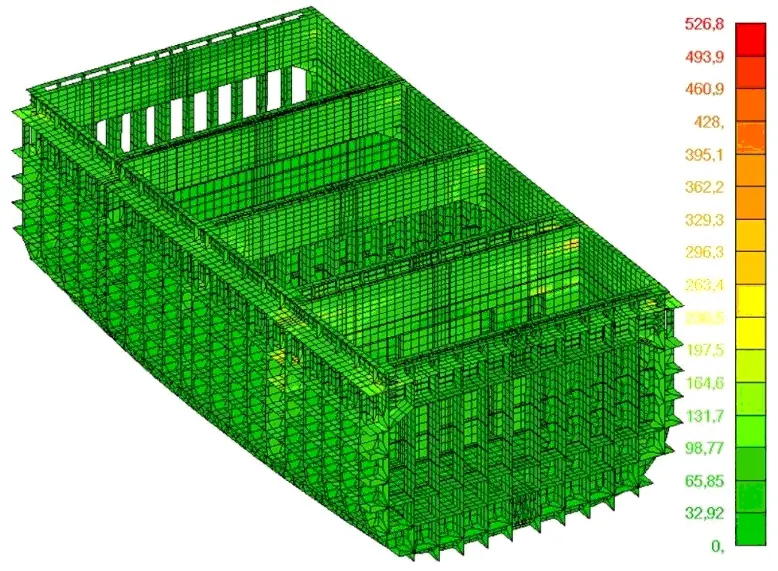
Rys. 5. Naprężenia zredukowane w modelu A i B, [MPa]
W celu porównania modeli zestawiono także maksymalne naprężenia w charakterystycznych elementach na pokładzie wytrzymałościowym modeli, których położenie zostało pokazane na poniższym rysunku. Wyniki zostały przestawione w tabeli.
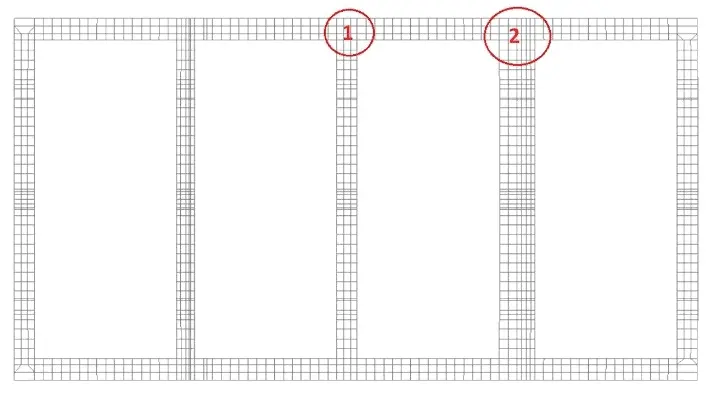
Rys. 6. Położenie wybranych elementów
Tab. 1. Naprężenia maksymalne w wybranych elementach pokładu
| Rejon | Naprężenia [MPa] | Model A | Model B | Δ [%] |
1 | Normalne | 60.0 | 44.2 | 26 |
| Ścinające | 120.2 | 79.7 | 34 | |
| Zredukowane | 208.3 | 138.2 | 34 | |
2 | Normalne | 117.1 | 93.2 | 20 |
| Ścinające | 166.6 | 104.7 | 37 | |
| Zredukowane | 298.7 | 209.3 | 30 |
Przeprowadzone badania wykazały, że stosowane w analizie wytrzymałości kadłuba masowców i zbiornikowców podejście ‘cargo-hold analysis’ nie oddaje rzeczywistej odpowiedzi konstrukcji kadłuba kontenerowca poddanego obciążeniom skręcającym. Jednocześnie, pomimo znacznego zwiększenia pracochłonności wykonania modelu, opracowana w Polskim Rejestrze Statków metoda analizy globalnej dostarcza wiarygodne i realistyczne wartości naprężeń i odkształceń skręcanego kadłuba kontenerowca.
Prezentacja pracy
Rozszerzona wersja powyższej analizy została zaprezentowana podczas konferencji MARTECH 2020 (16-19 Listopada, Lizbona, Portugalia), i dostępna będzie w opublikowanych materiałach pokonferencyjnych.
W Pionie Naukowo-Badawczym została opracowana teoria obliczeń krzywej ramion statku swobodnie pływającego, dostępna w Technical Report no 71.
Wg tej teorii zmodyfikowany został program WinSEA, używany w PRS do obliczeń stateczności statku. Modyfikacji dokonał autor programu dr Andrzej Laskowski. Użytkownik ma do wyboru trzy opcje obliczeń krzywej ramion: 1) “inżynierską”, związaną z osią Ox’ lub Ox”, 2) “fizyczną”, związaną z osią Oy lub Oy’, i 3) “naturalną”, związaną z osią Oz’, tożsamą z krzywą ramion “minimalnej stateczności”. Jest też zerowa opcja “maksimum stateczności”, dla statku o stałym przegłębieniu, normalnie niestosowana.
Układ Ox’yz’ dotyczy statku przegłębionego; związany jest PS i wodnicą w położeniu wyprostowanym. Układ Ox”y’z’ jest układem obróconym względem układu Ox’yz’ wokół osi Oz’ o kąt azymutu y. Obydwa układy są sztywno związane z jednostką.
Obliczenia wykonane dla statków o kształtach konwencjonalnych pokazują, że wybór osi referencyjnej nie ma znaczenia. Ma natomiast pewne znaczenie dla platform, ze względu na mały stosunek L/B, z czym wiąże się mała różnica między statecznością wzdłużną i poprzeczną. W wypadku platform ze wstępnym przechyłem znaczenie ma burta, na którą przechyla się platforma, gdy jest przechylana w stronę wstępnego przechyłu, krzywa ramion istnieje w całym zakresie przechyłów, Gdy przechylana jest na burtę przeciwną do wstępnego przechyłu, w pewnym sąsiedztwie zera krzywa ramion może być nieokreślona, z powodu braku zrównoważenia wzdłużnego. Wiąże się to z małym stosunkiem L/B, a ściślej – z małym stosunkiem głównych momentów bezwładności wodnicy w położeniu wyprostowanym Jy/Jx. Problemu tego nie ma dla jednostek bez wstępnego przechyłu – krzywe ramion istnieją na obydwie burty.
W przedziale, gdzie krzywa ramion jest nieokreślona jednostka jest niestabilna względem kąta skręcenia, tzn. statek może samoczynnie obrócić się o 180° względem osi z’, przyjmując przechył na stronę wstępnego przechyłu, gdzie statek jest stabilny (ma dodatnią wzdłużną wysokość metacentryczną) względem kąta skręcenia. Ta niestabilność względem kąta skręcenia jest niekorzystna dla bezpieczeństwa statku.
Poniżej przedstawiono krzywe ramion dla trzech statków i dwóch platform samopodnośnych.
 Rys. 1. Badany kuter rybacki
Rys. 1. Badany kuter rybacki
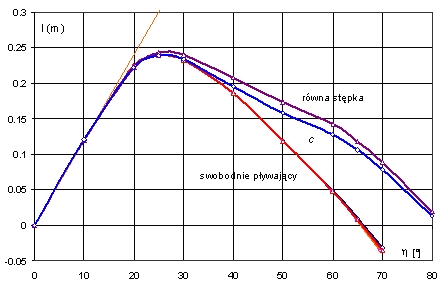
Rys. 2. Krzywe ramion prostujących kutra
Krzywa c na Rys. 2 dotyczy stałego przegłębienia, jakie występuje w położeniu równowagi.
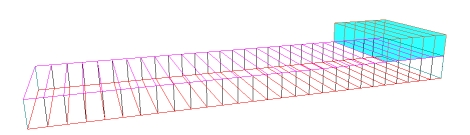 Rys. 3. Barka
Rys. 3. Barka
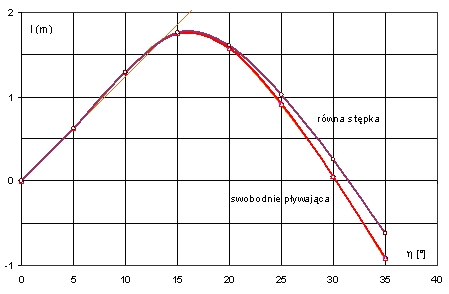 Rys. 4. Krzywe ramion prostujących barki
Rys. 4. Krzywe ramion prostujących barki
Dla jednostek bez wstępnego przechyłu, krzywe ramion są antysymetryczne.
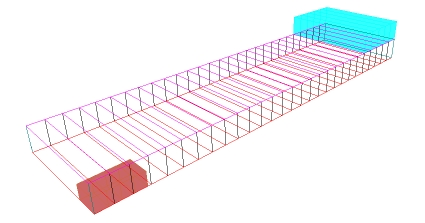
Rys. 5. Barka w stanie uszkodzonym
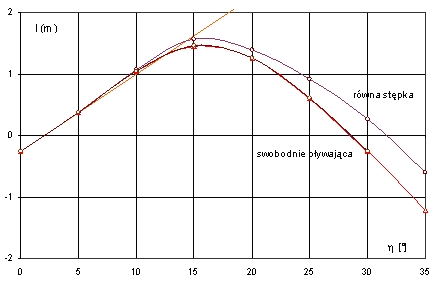 Rys. 6. Krzywe ramion prostujących barki w stanie uszkodzonym dla przechyłów na prawą burtę
Rys. 6. Krzywe ramion prostujących barki w stanie uszkodzonym dla przechyłów na prawą burtę
(w stronę wstępnego przechyłu)
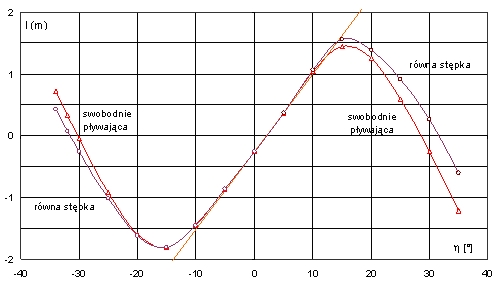
Rys. 7. Krzywe ramion barki w stanie uszkodzonym dla przechyłów na obie burty
Dla jednostek ze wstępnym przechyłem, krzywe ramion na obie burty są różne. Na burtę przeciwną do wstępnego przechyłu są większe, przy czym w pewnym sąsiedztwie zera krzywa ramion minimalnej stateczności nie istnieje z braku możliwości wzdłużnego zrównoważenia. W wypadku statków konwencjonalnych, przedział nieciągłości także istnieje, lecz jest niezauważalny, rzędu minut kątowych.
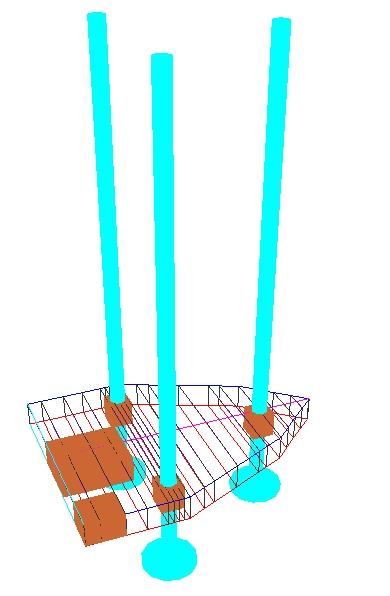 Rys. 8. Platforma I w stanie uszkodzonym, L/B = 1,36, Jy/Jx = 1,73
Rys. 8. Platforma I w stanie uszkodzonym, L/B = 1,36, Jy/Jx = 1,73
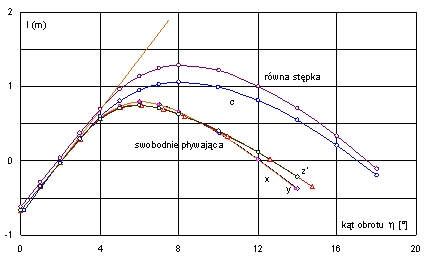
Rys. 9. Krzywe ramion platformy I dla przechyłów na prawą burtę (w stronę wstępnego przechyłu)
Krzywa c na Rys. 9 dotyczy stałego przegłębienia, jak w położeniu równowagi.
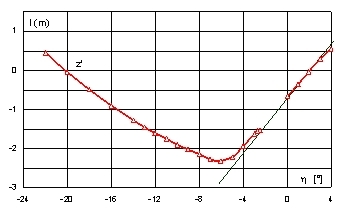 Rys. 10. Krzywa ramion platformy I swobodnie pływającej dla przechyłów na lewą burtę
Rys. 10. Krzywa ramion platformy I swobodnie pływającej dla przechyłów na lewą burtę
Dla przechyłów na lewą burtę, w przedziale a’ Î á0, -2,5°ñ krzywa ramion nie istnieje. Poza tym przedziałem, absolutne wartości ramion są większe, co widać lepiej na Rys. 12. Na wykresie zbiorczym (Rys. 12) słabo widać przedział nieciągłości dla krzywej minimalnej stateczności (krzywa z’).
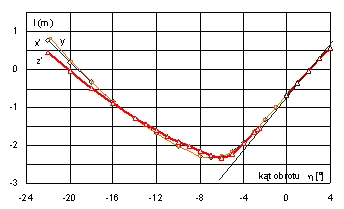
Rys. 11. Krzywe ramion platformy I dla przechyłów na lewą burtę
Zwraca uwagę, że krzywe ramion dla osi referencyjnej x’ i y niewiele różnią się od siebie. Tak jest w każdym przypadku, co widać na załączonych wykresach krzywych ramion. Wynika to stąd, że osie obrotu e dla tych krzywych są bardzo zbliżone do siebie. Obie te krzywe niewiele się różnią od krzywej minimalnej stateczności (krzywej z’).
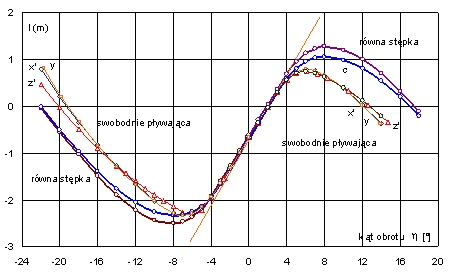
Rys. 12. Krzywe ramion platformy I dla przechyłów na obie burty
Normalnie, dla zadanego kąta przechyłu wzdłużne zrównoważenie statku zachodzi dla czterech kątów skręcenia (czterech azymutów), odpowiadających przechyłom poprzecznym na lewą i prawą burtę oraz przechyłom wzdłużnym (przegłębieniom), na dziób i rufę. Na dwóch pierwszych występują minima ramion dynamicznych, na drugich – maksima.
W przedziale, gdzie krzywa ramion nie istnieje, występują jedynie dwa miejsca zerowe, odpowiadające minimum i maksimum ramienia dynamicznego ld (Rys. 13). Minimum odpowiada przechyłowi na stronę wstępnego przechyłu. Otoczenie maksimum odpowiada przechyłom niestatecznym względem kąta skręcenia. Oznacza to, że statek samoczynnie obróci się wokół osi z’ do azymutu, gdzie występuje minimum ramienia dynamicznego ld. Gdy kąt przechyłu będzie większy od 2,5°, punkt B na Rys. 13 przejdzie na stronę ujemną. Pojawią się więc cztery miejsca zerowe krzywej le, którym będą odpowiadały naprzemiennie minimum i maksimum krzywej ramion dynamicznych ld.
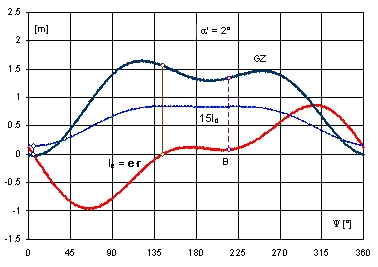
Rys. 13. Przebieg charakterystyk stateczności platformy I w funkcji kąta skręcenia Y dla a’ = 2°
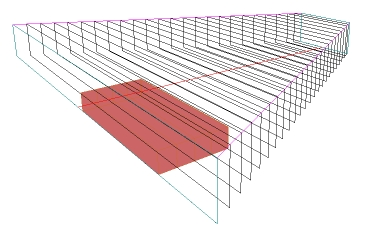
Rys. 14. Platforma II w stanie uszkodzonym, L/Bmax = 0,805, Jy/Jx = 1,06
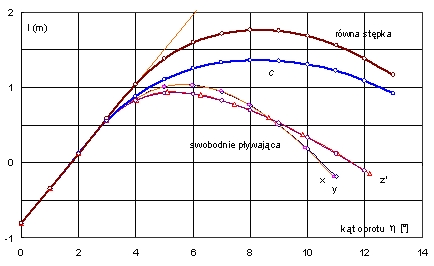
Rys. 15. Krzywe ramion platformy II dla przechyłów na prawą burtę (w stronę wstępnego przechyłu)
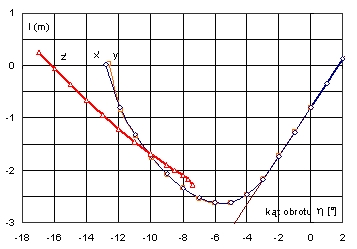
Rys. 16. Krzywe ramion platformy II dla przechyłów na lewą burtę
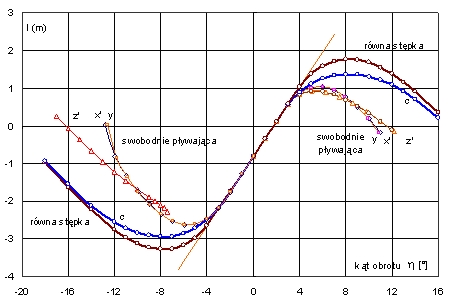
Rys. 17. Krzywe ramion platformy II dla przechyłów na obie burty
Ze względu na stosunek L/Bmax mniejszy od 1, przedział nieciągłości dla krzywej minimalnej stateczności (krzywa z’) dla przechyłów na lewą burtę jest znacznie dłuższy niż w poprzednim wypadku, równy -7,4°, zamiast -2,5°. Inaczej mówiąc, w przedziale a’ Î á0, -7,5°ñ krzywa minimalnej stateczności nie istnieje. Z kolei, dla osi referencyjnych Ox’ i Oy krzywe ramion nie istnieją dla kątów poniżej -13° (Rys. 16, Rys. 17). Nie są to jednak krzywe minimalnej stateczności, choć mają to samo pole pomiędzy położeniem równowagi, a zakresem krzywej ramion, co krzywa z’.
Jak poprzednio, w przedziale gdzie krzywa ramion nie istnieje, występują jedynie dwa miejsca zerowe, odpowiadające minimum i maksimum ramienia dynamicznego ld (Rys. 18).
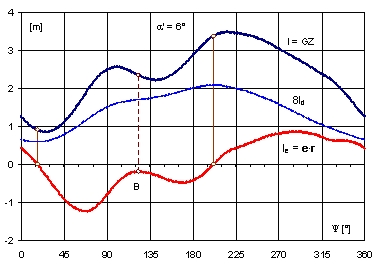
Rys. 18. Przebieg krzywych l, ld i le w funkcji kąta skręcenia Y dla kąta przechyłu a‘ = 6°
Rys. 19 pokazuje przebieg charakterystyk stateczności dla kąta przechyłu a‘ = 6° w funkcji azymutu dla osi referencyjnej Ox”. Identyczne charakterystyki występują dla osi referencyjnej Oy‘. Widzimy, że różnią się one od przebiegu tych charakterystyk dla osi referencyjnej Oz‘ (Rys. 18). Tym niemniej, obydwa wskazują na wspólne cechy – dla zadanego kąta przechyłu minimum i maksimum ramion dynamicznych występują przy tym samych kątach skrętu (azymutu).
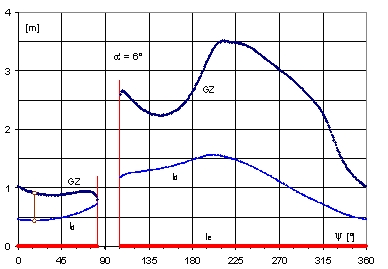 Rys. 19. Przebieg ramienia prostującego l º GZ oraz dynamicznego ld platformy II
Rys. 19. Przebieg ramienia prostującego l º GZ oraz dynamicznego ld platformy II
w funkcji azymutu Y, dla przechyłu mniejszego od krytycznego
Z Rys. 19 wynika ponadto, że dla kąta przechyłu a‘ = 6° platformy nie da się zrównoważyć wzdłużnie, gdy azymut jest z przedziału y Î á86°, 106°ñ.
Z przeprowadzonych obliczeń wynika kilka dalszych wniosków:
a) w początkowym zakresie stateczności wszystkie opcje obliczeniowe, łącznie ze stałym przegłębieniem, są praktycznie tożsame
b) wybór osi referencyjnej nie zmienia kierunku momentu prostującego, ani pola pod krzywą ramion pomiędzy położeniem równowagi a zakresem stateczności, które jest najmniejsze z możliwych. Jest to cecha statku swobodnie pływającego
c) gdy statek ma wstępny przechył, w pewnym sąsiedztwie zera dla przechyłów na przeciwległą burtę, zależnym od stosunku L/B, nie można wyznaczyć krzywej ramion minimalnej stateczności, gdyż nie da się statku wzdłużnie zrównoważyć
d) dla statku swobodnie pływającego znaczenie ma tylko jedna krzywa ramion, dla przechyłów poprzecznych. Dla innych azymutów krzywe ramion mają przedziały nieciągłości
Dla statków konwencjonalnych nie ma więc rewolucji – jakkolwiek nie obliczać krzywych ramion statku swobodnie pływającego, są takie same. Jest natomiast rewolucyjny wniosek dla platform – jest tylko jedna krzywa ramion minimalnej stateczności, związana z osią referencyjną Oz’. Inaczej mówiąc, dla platform swobodnie pływających nie istnieją krzywe ramion dla różnych azymutów, czego wymagają przepisy.
Opracowanie Common Structural Rules dla masowców i zbiornikowców
W Pionie Naukowo-Badawczym został opracowany program komputerowy do automatycznego przykładania obciążeń do konstrukcji masowca i zbiornikowca, zdefiniowanych w przepisach Common Structural Rules for Bulk Carriers oraz Common Structural Rules for Double Hull Oil Tankers. Program wspomaga pracę inspektorów w procesie wykonywania obliczeń wytrzymałości strefowej modułu kadłuba metodą elementów skończonych.
Poniżej przedstawiono przykłady rozkładów obciążeń na module środkowym kadłuba masowca, obliczonych przy pomocy opracowanego programu (dla stanu Alternate Load oraz Alt Block Load).
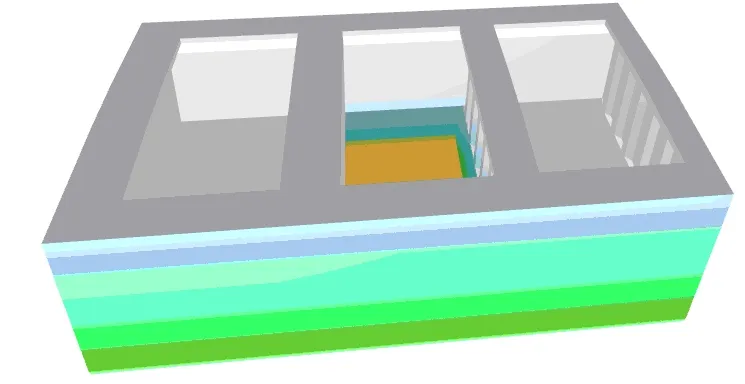 | 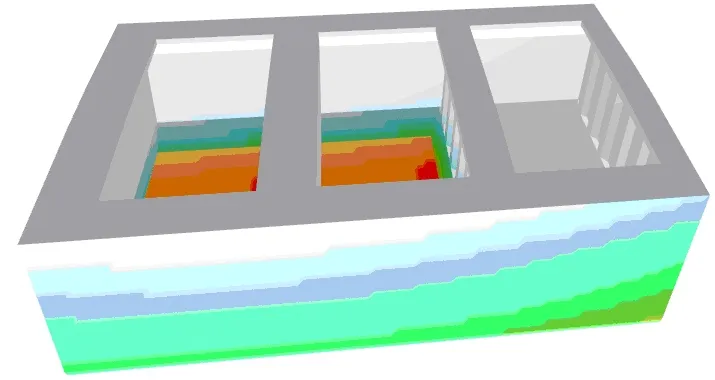 |
Rys. 1 Rozkład ciśnień dla stanu Alternate Load – F2 oraz Alt-Block Load – H1
Rozkład obciążeń umożliwia dokonanie analizy wielkości naprężeń w elementach rozpatrywanego modułu kadłuba statku. Poniższe rysunki przedstawiają rozkład naprężeń zredukowanych dla zadanych obciążeń oraz wielkości przemieszczeń (przemieszczenia zostały zwiększone 50-krotnie w stosunku do skali rysunku).
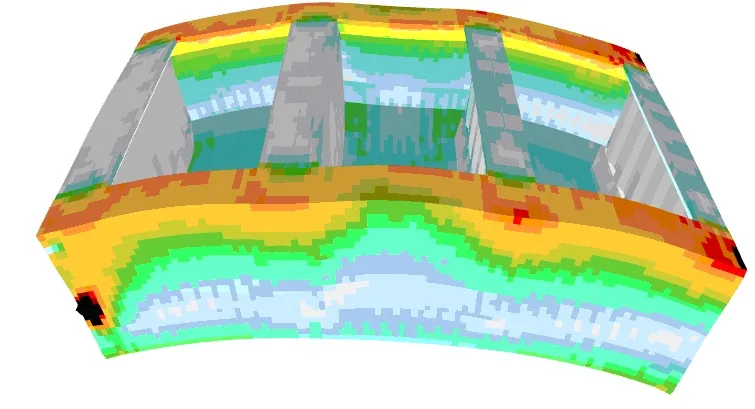 | 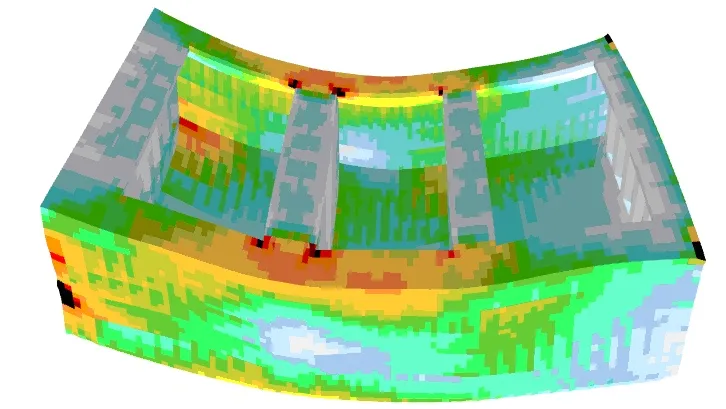 |
Rys. 2 Rozkład naprężeń zredukowanych dla stanu Alternate Load – F2 (hogging) oraz Alt-Block Load – H1 (sagging)
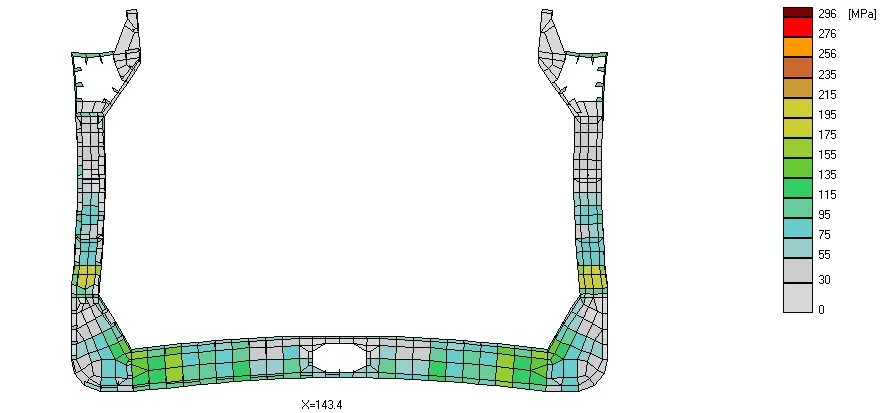
Rys. 3 Rozkład wartości naprężeń w przekroju wręgowym
Obciążenia falowe
Opracowanie procedur automatycznego zadawania obciążeń na elementach skończonych opisujących rozpatrywany moduł kadłuba dało możliwość wykonania obliczeń konstrukcji statku dla rzeczywistych obciążeń, występujących w dowolnych warunkach falowania. Obciążenia te to, między innymi, obciążenia od ładunku, na który oprócz sił grawitacyjnych działają siły bezwładności spowodowane ruchem statku na fali, obciążenia generowane falą na zwilżonej powierzchni itp. Obliczenia naprężeń przeprowadzane są w dziedzinie czasu.
Poniższy rysunek przedstawia zmieniający się w czasie rozkład ciśnień falowych.
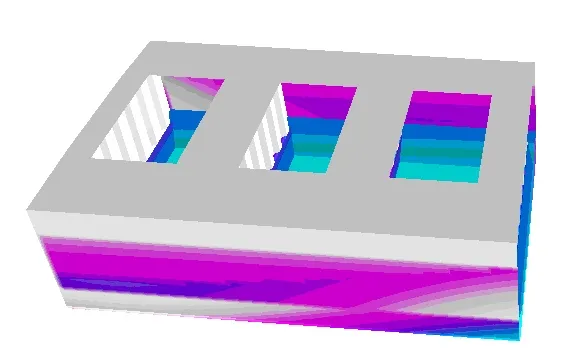 |  | 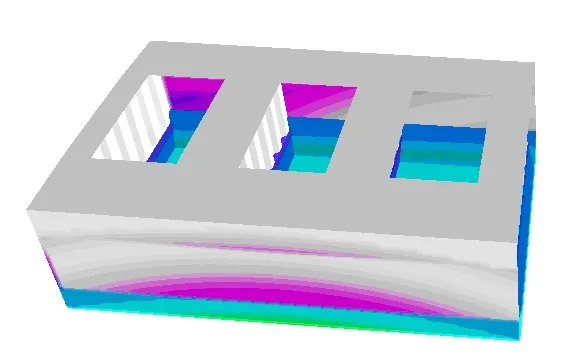 |
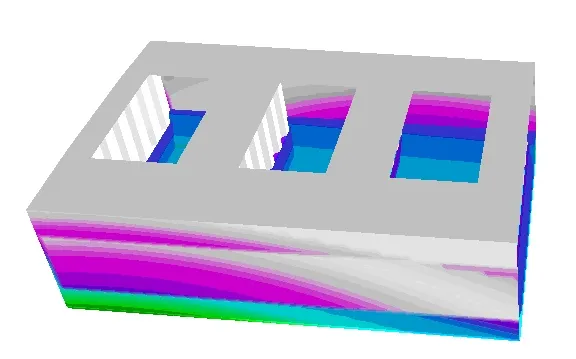 |  | 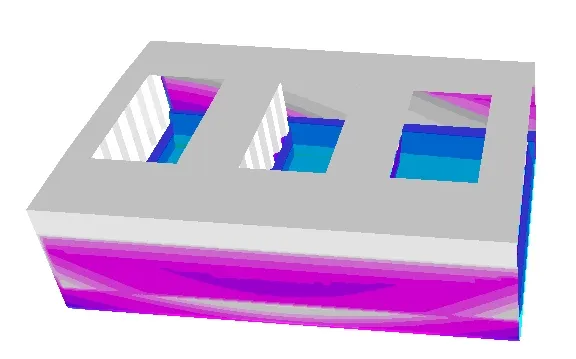 |
Rys. 4 Rozkład ciśnień falowych dla t=0, t=1/5T,…., t=T
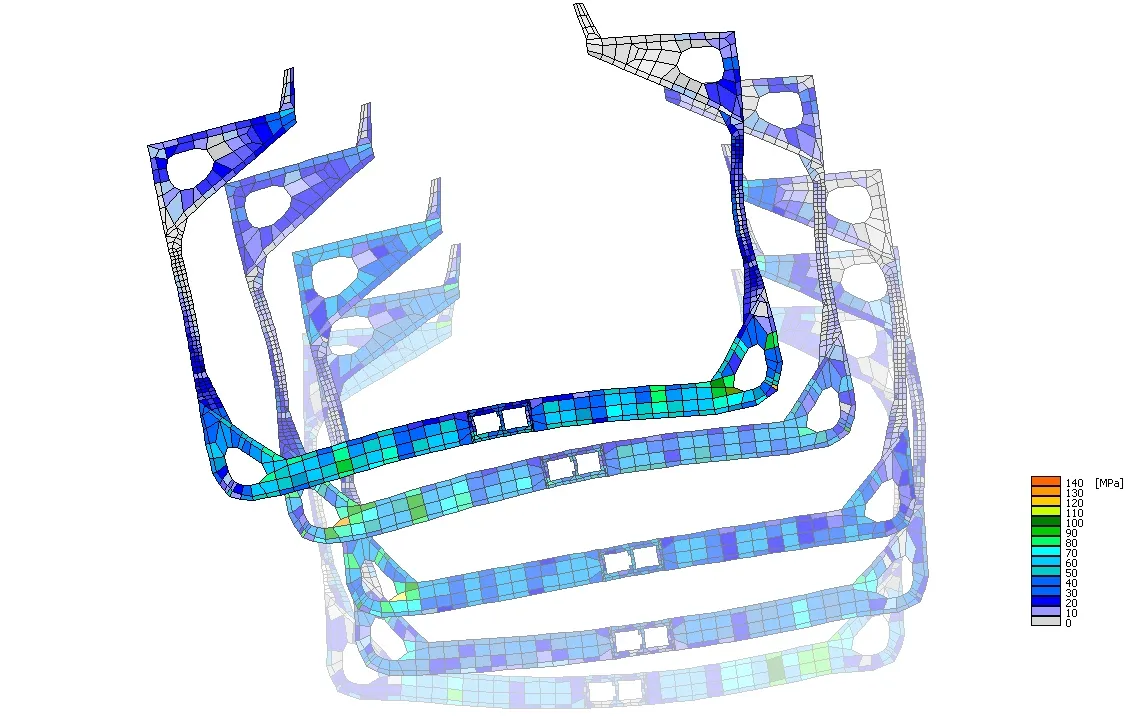
Rys. 5 Zmiana przemieszczenia elementów konstrukcji i zmiana rozkładu naprężeń w przekroju wręgowym spowodowana obciążeniami falowymi modułu konstrukcji w dziedzinie czasu
Prognozowanie naprężeń w konstrukcji kadłuba statku
W konsekwencji powstało oprogramowanie, które daje możliwość wykonania prognozy długoterminowej zachowania statku na fali i analizy wielkości naprężeń, jakie mogą wystąpić w cyklu życia statku. W obliczeniach wykorzystano tak zwaną metodę współczynników wpływu. Metoda polega na podziale konstrukcji kadłuba na panele (większe od elementów skończonych), zadaniu jednostkowych obciążeń i wyliczeniu wielkości wpływu obciążeń jednostkowych na naprężenia w badanych elementach konstrukcji.
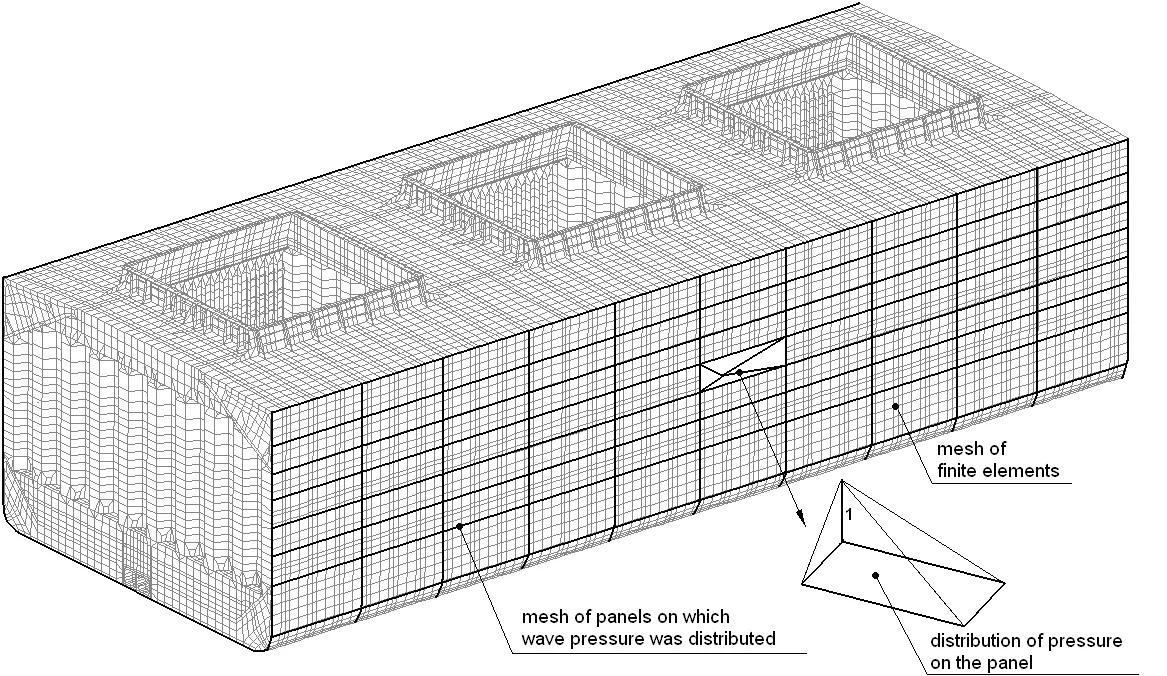
Rys. 6 Siatka elementów zastosowanych w metodzie współczynników wpływu
 | 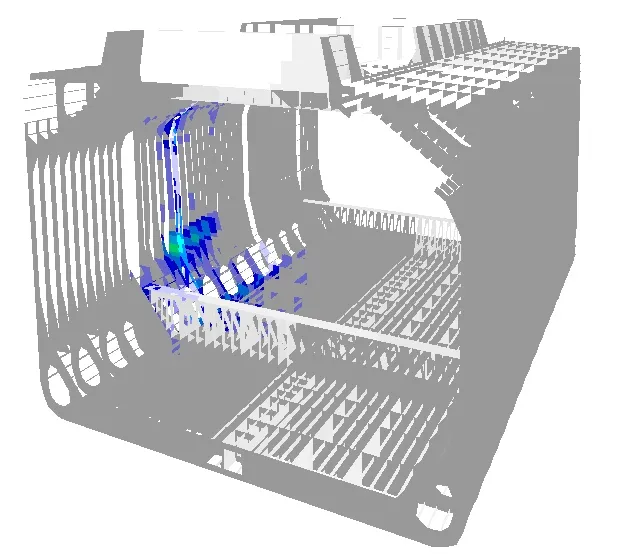 |
Rys. 7 Rozkład jednostkowego ciśnienia na wybranym elemencie poszycia zewnętrznego i reakcja w postaci rozkładu naprężenia w konstrukcji na to jednostkowe ciśnienie
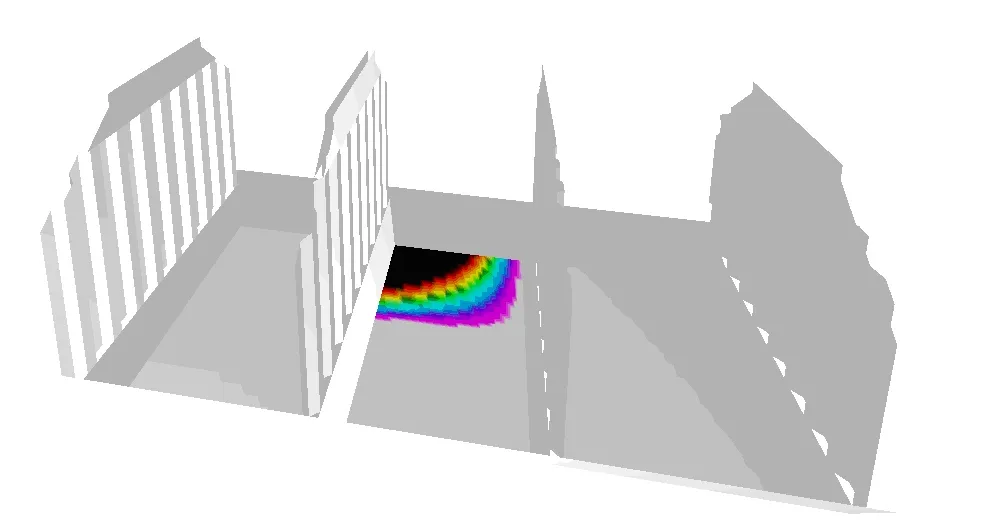 |  |
Rys. 8 Rozkład jednostkowego ciśnienia na wybranym elemencie konstrukcji i jego wpływ na rozkład naprężenia w konstrukcji
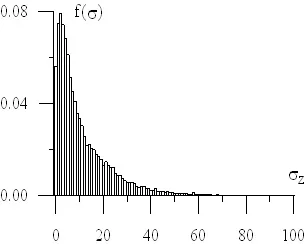
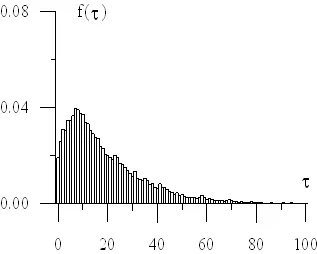
Symulacje naprężeń w różnych stanach morza dają możliwość opracowania funkcji gęstości rozkładu prawdopodobieństwa dla naprężeń w poszczególnych elementach konstrukcji statku. Przykłady takich rozkładów przedstawiono na poniższych wykresach.
|
|
Rys. 9 Funkcja rozkładu gęstości naprężeń zredukowanych i stycznych w badanym punkcie konstrukcji